На днях была крайняя необходимость собрать двоичный счётчик на JK-триггерах, и после того как мне надоело делать это методом научного тыка, решил обратиться к старым лекциям по цифровым устройствам. После долгого втыкания в лекции решил написать эту статью, так как в лекциях всё было сильно запутано, а в сети я не смог найти подробной методики синтеза. А начать стоит наверное с того, что основной проблемой при синтезе для меня стало заполнение диаграмм Вейча, ну в общем обо всём по порядку и поподробнее...
Итак, счётчик на триггерах можно реализовать практически с любым количеством разрядов и любой таблицей переключения. Для примера будем собирать двоичный синхронный счётчик, считающий до 12, именно его мне нужно было собрать на днях). Поехали...
Исходные данные:
Сколько у нас будет выходов? log12(2)=3.58? , наверное всё-таки четыре)
Как уже было сказано счётчик будет считать до 12, т.е. его таблица переключения будет такой:
| n | Q1 | Q2 | Q3 | Q4 |
| 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 | 0 |
| 5 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 |
| 8 | 0 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 |
| 10 | 0 | 1 | 0 | 1 |
| 11 | 1 | 1 | 0 | 1 |
| 12 | 0 | 0 | 1 | 1 |
| 13 | 0 | 0 | 0 | 0 |
После двенадцатого такта счётчик возвращается в первоначальное положение. Дополним таблицу переключения счётчика столбцами для следующего такта, т.е. то что было на выходе в первом такте, теперь будет в нулевом:
| n | Q1 | Q2 | Q3 | Q4 | n+1 Q1 | n+1 Q2 | n+1 Q3 | n+1 Q4 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 |
| 3 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 4 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 5 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
| 7 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 |
| 8 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 9 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 10 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 11 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 |
| 12 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 13 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
Тут вроде бы всё понятно, просто подняли основную таблицу на один такт.
Теперь то, что долго не давало мне покоя, что такое диаграмма Вейча?
Диаграмма Вейча - такая табличка, которая позволяет минимизировать количество элементов схемы, путём не сложных преобразований.
Каждая клетка диаграммы соответствует набору переменных функции в ее таблице истинности.
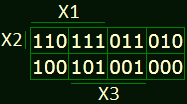
Для двух переменных:

Теперь то, что долго не давало мне покоя, что такое диаграмма Вейча?
Диаграмма Вейча - такая табличка, которая позволяет минимизировать количество элементов схемы, путём не сложных преобразований.
Каждая клетка диаграммы соответствует набору переменных функции в ее таблице истинности.
Для двух переменных:

Прошу обратить внимание на вот какой факт значения в этих таблицах указаны чтобы показать соответствие таблице истинности(переключения), на самом деле так она не заполняется...
Для трёх переменных:
Для трёх переменных:

Ага, а вот и для четырёх переменных:
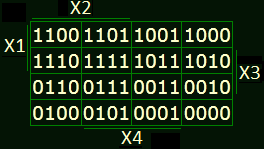
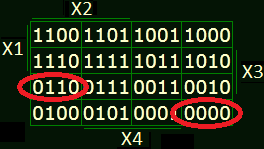
X1X2X3X4 соответствуют Q1Q2Q3Q4.
Смотрим, в нулевом такте(n=0) наша функция состоящая из Q1Q2Q3Q4 равна 0000, значит нашей функции соответствует клетка диаграммы 0000, в первом такте - клетка в правом верхнем углу,а в шестом такте 0110, всё просто.

Смотрим, в нулевом такте(n=0) наша функция состоящая из Q1Q2Q3Q4 равна 0000, значит нашей функции соответствует клетка диаграммы 0000, в первом такте - клетка в правом верхнем углу,а в шестом такте 0110, всё просто.

Для четырёх выходов будет четыре прикладных диаграммы, начнём их заполнять.
Заполняем для Q1 по такой методике:
1.Находим ячейку в диаграмме соответствующую значению всей нашей функции в нулевом такте,т.е в нулевом такте Q1Q2Q3Q4=0000, находим эту ячейку.
2.Записываем в найденную ячейку значения Q1 в n-ом такте и в n+1-вом, т.е если в нулевом такте Q1=0, а в первом(следующем) Q1=1, записываем в ячейку 0000 значения 01.
3.Если в таблице переключения некоторых значений функций нет, например для четырёх разрядов по умолчанию используется 16 комбинаций(0-15), а у нас 13(0-12), ячейки прикладной диаграммы соответствующие этим значениям функции заполняются символом "X"(неопределённое значение).
Заполняем диаграммы:
Как видно из таблицы переключения и прикладных диаграмм Вейча, комбинации 1111(15),1110(14),1101(13) являются неопределёнными, мы специально их выбросили, чтобы счёт шёл не до 15 , а до 12.
Прикладные диаграммы заполнены(надеюсь всё понятно), теперь нужно получить уравнения входов и начать собирать схему.
Заполняем для Q1 по такой методике:
1.Находим ячейку в диаграмме соответствующую значению всей нашей функции в нулевом такте,т.е в нулевом такте Q1Q2Q3Q4=0000, находим эту ячейку.
2.Записываем в найденную ячейку значения Q1 в n-ом такте и в n+1-вом, т.е если в нулевом такте Q1=0, а в первом(следующем) Q1=1, записываем в ячейку 0000 значения 01.
3.Если в таблице переключения некоторых значений функций нет, например для четырёх разрядов по умолчанию используется 16 комбинаций(0-15), а у нас 13(0-12), ячейки прикладной диаграммы соответствующие этим значениям функции заполняются символом "X"(неопределённое значение).
Заполняем диаграммы:
Q1,Q1n+1
| Q2,Q2n+1
| ||||||||||||||||||||||||||||||||
Q3,Q3n+1
| Q4,Q4n+1
|
Как видно из таблицы переключения и прикладных диаграмм Вейча, комбинации 1111(15),1110(14),1101(13) являются неопределёнными, мы специально их выбросили, чтобы счёт шёл не до 15 , а до 12.
Прикладные диаграммы заполнены(надеюсь всё понятно), теперь нужно получить уравнения входов и начать собирать схему.
Для того чтобы собрать схему нужно составить уравнения входов, для того чтобы составить уравнения входов понадобиться заполнить диаграммы Вейча(уже не прикладные),а диаграммы Вейча для входов необходимо заполнять по прикладным диаграммам и характеристической таблице выбранного триггера...тьфу, ничего не понятно...а ну и ладно, поехали...
Вот характеристическая таблица JK триггера:
| Qn»Qn+1; | Jn | Kn |
| 00 | 0 | X |
| 01 | 1 | X |
| 10 | X | 1 |
| 11 | X | 0 |
Заполняем диаграммы Вейча исходя из этой таблицы, если в прикладной диаграмме стоит "00", то в диаграммах входов для J будет "0", а для K будет "X".
J1
| K1
| ||||||||||||||||||||||||||||||||
J2
| K2
| ||||||||||||||||||||||||||||||||
J3
| K3
| ||||||||||||||||||||||||||||||||
J4
| K4
|
Ну что-же, приступим к минимизации и получению уравнений входов, по которым легко соберём схему.
Перед минимизацией нужно знать, что состояние "X" является неопределённым, т.е нам всё равно что это будет 0 или 1, поэтому его можно определить так как удобно нам.
Те кто хоть раз сталкивались с минимизацией при помощи диаграмм Вейча или карт Карно, знают как это делать и для них трудностей возникать не должно, а вот для тех кто сталкивается с этим впервые опишу вкратце.
Минимизация заключается в объединении ячеек диаграммы в группы из единиц или нулей, после чего с таких диаграмм считываются уравнения входов. Если объединение происходит по нулям, то потом при считывании над всеми значениями ставится инверсия.
Мы будем объединять ячейки в группы из единиц, следует учесть , что чем больше клеток в группе, тем компактнее будет уравнение, но нельзя допускать чтобы в группе был и ноль (0) и единица (1), тогда уравнение будет не правильным, это следует учесть при доопределении состояний "X".
Правила объединения в группы :
1.Соседними являются не только клетки, расположенные рядом по вертикали и по горизонтали, но и клетки на противоположных концах диаграммы Вейча(или карты Карно)
2.Клетки могут объединяться в группы по 2, по 4 по 8 (2ˆk) только в прямоугольной конфигурации.
3.Одни и те же клетки могут входить в несколько групп.
Начнём группировку с того, что определим состояния "X" для наибольшего количества единиц в группе:
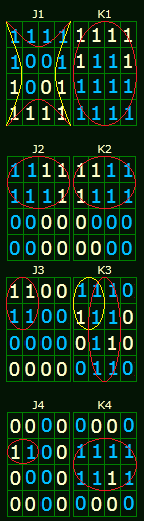
Далее необходимо произвести считывание уравнений входов с диаграмм(карт) входов. При считывании аргументы функции в группе перемножаются, а сами группы складываются. Для J1 у нас получилось две группы возьмём первую, внимательно смотрим на её содержание...если аргумент(Q1,Q2,Q3 или Q4) во всей группе (в каждой клетке группы) равен единице, то он записывается в уравнение как есть, если нулю то с инверсией, а если меняется с 1 в 0 или из 0 в 1, то не записывается вовсе...Для простоты такого перехода вернёмся к таблице соответствия :


Мысленно выделим эту группу на таблице соответствия, и посмотрим какие аргументы остаются постоянными, а какие меняются.
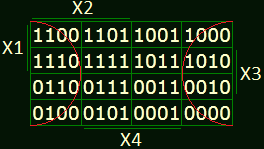

Всё ясно, Q4 - всё время равен нулю, а остальные аргументы изменяются, значит так и запишем J1=¯Q4+...
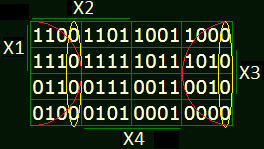
Сразу скажу, что если группа состоит из одного элемента, то уравнение будет состоять из четырех, если группа состоит из двух элементов, то уравнение её описывающее будет из трёх множителей, если же из четырёх, то два, а восемь - это один какой-то элемент(для случая с четырьмя аргументами). Иногда группа охватывает всю диаграмму Вейча как K1, тогда функция равна либо нулю, либо единице в зависимости от того, чем заполнена карта.(для нашего случая K1=1)
Вернёмся к J1, так как у нас две группы определяющие вход J1, запишем полное уравнение, посмотрев в таблицу соответствия получаем J1=¯Q4+¯Q3.
Такими же не сложными действиями получим остальные уравнения:
J1=¯Q4+¯Q3, K1=1, J2=Q1, K2=Q1, J3=Q1*Q2, K3=Q1*Q2+Q4, J4=Q1*Q2*Q3, K4=Q3
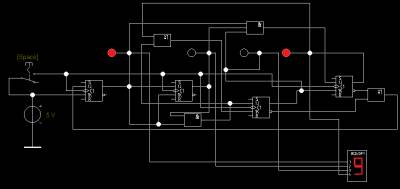
Отлично, теперь можно собрать схему и посмотреть как это работает:

Вернёмся к J1, так как у нас две группы определяющие вход J1, запишем полное уравнение, посмотрев в таблицу соответствия получаем J1=¯Q4+¯Q3.
Такими же не сложными действиями получим остальные уравнения:
J1=¯Q4+¯Q3, K1=1, J2=Q1, K2=Q1, J3=Q1*Q2, K3=Q1*Q2+Q4, J4=Q1*Q2*Q3, K4=Q3
Отлично, теперь можно собрать схему и посмотреть как это работает:
Схема собранная в Electronics WorkBench 5.12 отлично работает, для дополнительной проверки временная диаграмма из OrCad 9:
Ну вот пожалуй и всё, надеюсь кому-нибудь это пригодиться, для страждущих вот схема WorkBench, если что-то не понятно, то на форум или пишите в комментах, спасибо за внимание.
Ну вот пожалуй и всё, надеюсь кому-нибудь это пригодиться, для страждущих вот схема WorkBench, если что-то не понятно, то на форум или пишите в комментах, спасибо за внимание.



 09.02.21 -
09.02.21 -  30.07.20 -
30.07.20 -  11.12.18 -
11.12.18 -  16.04.17 -
16.04.17 -  05.05.16 -
05.05.16 -