Основное отличие вычитающих счётчиков от суммирующих - их таблица переключений, если у суммирующего счётчика в нулевом состоянии 0, а в первом 1(и так до модуля счёта), то у вычитающего в нулевом - модуль счёта(в данном примере  12), в первом (модуль счёта - 1), и так до нуля..

Исходные данные:
Сколько у нас будет выходов? log12(2)=3.58? Опять 4
Счётчик будет считать с 12 до нуля, а значит его таблица переключения будет такой:

n	Q1	Q2	Q3	Q4
0	0	0	1	1
1	1	1	0	1
2	0	1	0	1
3	1	0	0	1
4	0	0	0	0
5	1	1	1	0
6	0	1	1	0
7	1	0	1	0
8	0	0	1	0
9	1	1	0	0
10	0	1	0	0
11	1	0	0	0
12	0	0	0	0
13	0	0	1	1

После двенадцатого такта счётчик возвращается в первоначальное положение. Дополним таблицу переключения счётчика столбцами для следующего такта, т.е. то что было на выходе в первом такте, теперь будет в нулевом:

n	Q1	Q2	Q3	Q4	n+1 Q1	n+1 Q2	n+1 Q3	n+1 Q4
0	0	0	1	1	1	1	0	1
1	1	1	0	1	0	1	0	1
2	0	1	0	1	1	0	0	1
3	1	0	0	1	0	0	0	1
4	0	0	0	1	1	1	1	0
5	1	1	1	0	0	1	1	0
6	0	1	1	0	1	0	1	0
7	1	0	1	0	0	0	1	0
8	0	0	1	0	1	1	0	0
9	1	1	0	0	0	1	0	0
10	0	1	0	0	1	0	0	0
11	1	0	0	0	0	0	0	0
12	0	0	0	0	0	0	1	1
13	0	0	1	1	1	1	0	1

Далее синтез ничем не отличается от синтеза суммирующего.
Заполняем прикладные диаграммы:

Теперь нужно получить уравнения входов и  начать собирать схему.
Нам необходимо определиться на каких триггерах делать схему. Снова делаем на JK триггерах, забегая вперёд скажу, что уравнения входов суммирующего и вычитающего счётчиков понадобятся для разработки реверсивного счётчика.

Вот характеристическая таблица JK триггера:

Qn»Qn+1;	Jn	Kn
00	0	X
01	1	X
10	X	1
11	X	0

Заполняем диаграммы Вейча для входов, исходя из характеристической таблицы, если в прикладной диаграмме стоит "00", то в диаграммах входов для J будет "0", а для K будет "X".

J1 X X X X X X X X 1 X 1 1 1 1 1 0	K1 1 1 1 1 1 X X 1 X X X X X X X X
J2 X X 0 0 X X X 0 X X 1 1 X X 1 0	K2 0 0 X X 0 X X X 1 X X X 1 1 X X
J3 0 0 0 0 X X X X X X X X 0 0 1 1	K3 X X X X 0 X X 0 0 X 1 1 X X X X
J4 0 X X 0 0 X X 0 0 X X 0 0 X X 1	K4 X 0 0 X X X X X X X 0 X X 0 1 X

Вот такие получились диаграммы Вейча для входов J и K нашего счётчика.
Доопределим состояния X, проведём минимизацию и получим уравнения входов.


Считываем уравнения входов:
J1=Q1+Q2+Q3+Q4, K1=1; J2=¯Q1Q3+¯Q1¯Q2Q4, K2=¯Q1Q2; J3=K3=¯Q1¯Q2; J4=K4=¯Q1¯Q2¯Q3;
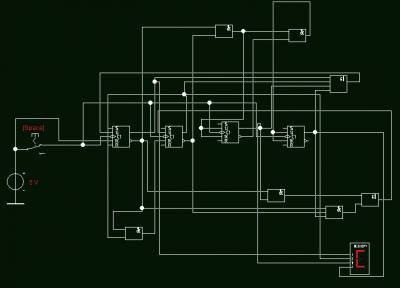
По уравнениям входов составим электрическую схему: