Описанные ранее счетчики Суммирующий счётчик и Вычитающий счётчик считают на увеличение или уменьшение, на практике часто необходимо менять направление счета в процессе работы. Счетчики, которые в процессе работы могут менять направление счета называются реверсивными. Где можно применить такой счётчик? Например в простом таймере-секундомере, для отображения на led-индикаторе уровня громкости,крутим переменный резистор по часовой стрелке значение уровня громкости увеличивается,против-уменьшается... Дело в вашей фантазии, применений-вагон.
Методика синтеза реверсивных счётчиков объединяет в себе методики синтеза суммирующего и вычитающего счётчиков, т.е. сначала синтезируются вычитающий и суммирующий счётчики, потом вводится сигнал отвечающий за направление счёта и все уравнения объединяются. Теперь подробнее: За основу берём две статьи суммирующий и вычитающий счётчики.
Как и ранее модуль счёта равен двенадцати. Для того чтобы не повторяться, я не буду заново описывать полную методику синтеза суммирующего и вычитающего счётчиков, опишу вкратце, если не понятно, читайте ранние статьи или пишите комментарии.
1.Суммирующий счётчик:
Таблица переключений:

Прикладные диаграммы Вейча:
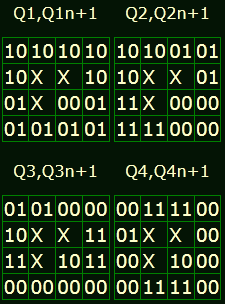
Характеристическая таблица JK триггера:
| Qn»Qn+1; | Jn |
Kn |
| 00 |
0 |
X |
| 01 |
1 |
X |
| 10 |
X |
1 |
| 11 |
X |
0 |
Заполняем диаграммы Вейча исходя из этой таблицы, если в прикладной диаграмме стоит "00", то в диаграммах входов для J будет "0", а для K будет "X".

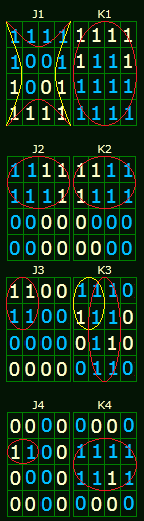
Получаем уравнения входов:
J1=¯Q4+¯Q3, K1=1, J2=Q1, K2=Q1, J3=Q1*Q2, K3=Q1*Q2+Q4, J4=Q1*Q2*Q3, K4=Q32.Вычитающий счётчик:
Составляем таблицу переключений:
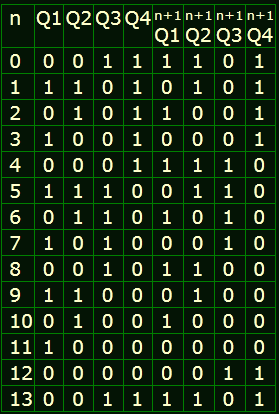
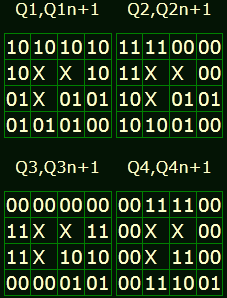
Пользуясь характеристической таблицей JK-триггера, заполняем диаграммы входов:

Производим минимизацию:

Считываем уравнения входов:
J1=Q1+Q2+Q3+Q4, K1=1; J2=¯Q1Q3+¯Q1¯Q2Q4, K2=¯Q1Q2; J3=K3=¯Q1¯Q2; J4=K4=¯Q1¯Q2¯Q3;
3.Реверсивный счётчик:
Теперь у нас есть уравнения входов для суммирующего и вычитающего счётчиков:
(+)
J1=¯Q4+¯Q3, K1=1, J2=Q1, K2=Q1, J3=Q1*Q2, K3=Q1*Q2+Q4, J4=Q1*Q2*Q3, K4=Q3
(–)
J1=Q1+Q2+Q3+Q4, K1=1; J2=¯Q1Q3+¯Q1¯Q2Q4, K2=¯Q1Q2; J3=K3=¯Q1¯Q2; J4=K4=¯Q1¯Q2¯Q3;
Эти уравнения нужно объединить и ввести в них сигнал направления счёта. В принцип такого управления вложено простое правило "что на ноль не умножь, всё равно будет ноль", как это понять? Очень просто, нам необходимо ввести сигнал P, от которого будет зависеть направление счёта, если P=1, то J1=(+)J1, а если P=0, то J1=(–)J1, реализуется это так:
J1=(P*(+)J1)+(¯P*(–)J1),
здесь (+)J1 это уравнение входа J1 для суммирующего счётчика,т.е. вот это J1=¯Q4+¯Q3, а (–)J1 - уравнение входа J1 для вычитающего счётчика,т.е. вот это J1=Q1+Q2+Q3+Q4.
Немного разобрались? Нет? Если простым языком то мы просто берём и умножаем уравнения входов суммирующего счётчика на P, а уравнения вычитающего на инверсный P, после чего складываем их.
Запишем полное уравнение входа J1 для реверсивного счётчика:
J1=((¯Q4+¯Q3)*P)+((Q1+Q2+Q3+Q4)*¯P),
когда P=1, J1=¯Q4+¯Q3, а когда P=0, J1=Q1+Q2+Q3+Q4.
Отлично, теперь всё должно быть понятно, записываем аналогично для всех входов:
J1=((¯Q4+¯Q3)*P)+((Q1+Q2+Q3+Q4)*¯P), K1=1;
J2=(Q1*P)+((¯Q1*Q3+¯Q1¯Q2*Q4)*¯P), K2=(Q1*P)+(¯Q1Q2¯P);
J3=(Q1*Q2*P)+(¯Q1¯Q2¯P), K3=((Q1*Q2+Q4)*P)+(¯Q1¯Q2¯P);
J4=(Q1*Q2*Q3*P)+(¯Q1¯Q2¯Q3¯P), K4=(Q3*P)+(¯Q1¯Q2¯Q3¯P).
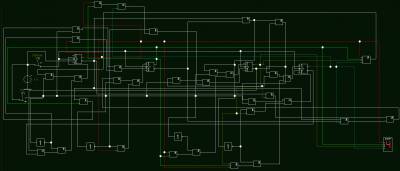
Уравнения входов составлены, пришло время собрать схему и посмотреть как это работает:
3.Реверсивный счётчик:
Теперь у нас есть уравнения входов для суммирующего и вычитающего счётчиков:
(+)
J1=¯Q4+¯Q3, K1=1, J2=Q1, K2=Q1, J3=Q1*Q2, K3=Q1*Q2+Q4, J4=Q1*Q2*Q3, K4=Q3
(–)
J1=Q1+Q2+Q3+Q4, K1=1; J2=¯Q1Q3+¯Q1¯Q2Q4, K2=¯Q1Q2; J3=K3=¯Q1¯Q2; J4=K4=¯Q1¯Q2¯Q3;
Эти уравнения нужно объединить и ввести в них сигнал направления счёта. В принцип такого управления вложено простое правило "что на ноль не умножь, всё равно будет ноль", как это понять? Очень просто, нам необходимо ввести сигнал P, от которого будет зависеть направление счёта, если P=1, то J1=(+)J1, а если P=0, то J1=(–)J1, реализуется это так:
J1=(P*(+)J1)+(¯P*(–)J1),
здесь (+)J1 это уравнение входа J1 для суммирующего счётчика,т.е. вот это J1=¯Q4+¯Q3, а (–)J1 - уравнение входа J1 для вычитающего счётчика,т.е. вот это J1=Q1+Q2+Q3+Q4.
Немного разобрались? Нет? Если простым языком то мы просто берём и умножаем уравнения входов суммирующего счётчика на P, а уравнения вычитающего на инверсный P, после чего складываем их.
Запишем полное уравнение входа J1 для реверсивного счётчика:
J1=((¯Q4+¯Q3)*P)+((Q1+Q2+Q3+Q4)*¯P),
когда P=1, J1=¯Q4+¯Q3, а когда P=0, J1=Q1+Q2+Q3+Q4.
Отлично, теперь всё должно быть понятно, записываем аналогично для всех входов:
J1=((¯Q4+¯Q3)*P)+((Q1+Q2+Q3+Q4)*¯P), K1=1;
J2=(Q1*P)+((¯Q1*Q3+¯Q1¯Q2*Q4)*¯P), K2=(Q1*P)+(¯Q1Q2¯P);
J3=(Q1*Q2*P)+(¯Q1¯Q2¯P), K3=((Q1*Q2+Q4)*P)+(¯Q1¯Q2¯P);
J4=(Q1*Q2*Q3*P)+(¯Q1¯Q2¯Q3¯P), K4=(Q3*P)+(¯Q1¯Q2¯Q3¯P).
Уравнения входов составлены, пришло время собрать схему и посмотреть как это работает:
Схема собранная в Electronics WorkBench 5.12 отлично работает. Как всегда для страждущих её можно скачать .
Удачи, если есть вопросы задавайте их на форуме или в комментариях.
Удачи, если есть вопросы задавайте их на форуме или в комментариях.


 09.02.21 -
09.02.21 -  30.07.20 -
30.07.20 -  11.12.18 -
11.12.18 -  16.04.17 -
16.04.17 -  05.05.16 -
05.05.16 -